Answer:
The slope is -3/4
Step-by-step explanation:
To find the slope of a line, you can use the "rise over run" method where you count how many units from one point to the next the line increases or decreases along the y-axis and place this number in the numerator of a fraction; then, count how many units to the left or right that same point is along the x-axis and place this number in the denominator. Simplify if necessary and that becomes the slope.
So, assuming each tick on the axes is 1 unit, to get from the leftmost point to the rightmost point, we go down 3 units on the y-axis ("rise" -3 units) and to the right 4 units ("run" 4 units). Therefore, the slope is -3/4
The method I like to use the most because it involves the actual math of finding a slope is plugging plotted points into the slope formula. The slope formula is
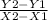where two points along the line (X1, Y1) and (X2, Y2) are used.
Again, assuming, each tick is 1 unit, the plotted points on the line in the image are (-2, 2) and (2, -1). Now, we plug these ordered pairs into the formula and solve:
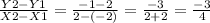
Therefore, the slope is -3/4