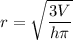Question

Using the formula for volume of a cone, express r in terms of V, h and pi

Answer 1

`r = \sqrt{\displaystyle(3V)/(h\pi)}`

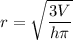
Explanation:

We are given the following information in the question.

Using the formula for volume of cone, we have to express r in terms of V, h and pi.

Formula:

`\text{Volume of cone, V} = \displaystyle(1)/(3)\pi r^2 h\\\\\text{where r is the radius of cone, h is the height of radius}`

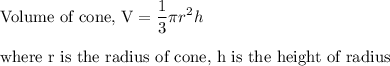
Now, we have to evaluate r, the radius of cone.

Rearranging the terms, we have,

Working:

`V = \displaystyle(1)/(3)\pi r^2 h\\\\r^2 = (3* V)/(\pi* h)\\\\r^2 = (3V)/(h\pi)\\\\r = \sqrt{(3V)/(h\pi)}`.

Thus, r in form of V, h and pi can be written as:

`r = \sqrt{\displaystyle(3V)/(h\pi)}`

Answer 2

The volume of the cone is one-third of the volume of the cylinder which is equal to the product of area of the base and the height. The equation is,

V = (1/3)(pi)(r^2)h

Dividing both sides of the equation by (1/3)(pi)(h) will give us,

3V/(pi)(h) = r^2

Taking the square-root of both sides,

r = sqrt(3V/(pi)(h))