Answer:
The given function is neither even nor odd.
Explanation:
A function is an even function if
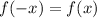
A function is an odd function if

From the given graph it is clear that graph is passing though the points (-3,2), (-1,2), (0,1/2), (1/2,0), (1,-1), (2,-1) and (3,1).
Here,
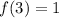
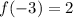
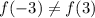 and
and
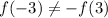
Since
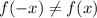 and
and
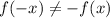 , therefore the given function is neither even nor odd.
, therefore the given function is neither even nor odd.