Answer: The correct option is second.
Step-by-step explanation:
The given function is,

If we graph a function is f(x), then its coordinates is defined as (x,f(x)).
When the graph of f(x) is reflect across the x-axis, then the the x-coordinate remains the same and the sign of y-coordinate is changed. It means after reflecting across the x-axis,
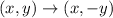
The given given equation can be written as,
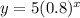
To find the equation of the graph after reflection across the x-axis multiply both sides by -1.
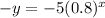
Because f(x)=y and g(x)=-y.

Therefore the second option is correct and the graph of both function is given below.