The answer is: "
x = 56 " .
____________________________Given : " 6/7 = 48/x ; Solve for "x" ;
Method 1): "Cross multiply" ;
6x = 7 * 48 ;
6x = 336 ;
Divide each side by "6" ; as follows:
__________________________________ 6x / 6 = 336 / 6 ;
______________________________________to get:
______________________________________ x = 56 .
______________________________________Method 2): Given: " 6/7 = 48/x " ; Solve for "x" ;
______________________________________ Cross-multiply:
______________________________________ 6x = 7 * 48 ;
______________________________________ Now, divide EACH SIDE of the equation by "6" ;
to isolate "x" on one side of the equation;
& to solve for "x" ;
______________________________________ 6x = 7 * 48 ;
______________________________________Divide EACH side of the equation by "6" :
______________________________________→ 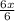
=
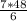
;
______________________________________On the "left-hand side" of the equation, the "6 's " cancel out to "1" ;
{since: (6÷6=1) ; & we are left with "x" on the left-hand side of the equation} ;
On the "right-hand side" of the equation; the "48" in the denominator
cancels out to an "
8" ; and the "6" cancels to a "1" ;
{since: (48÷6=8); & (6÷6=1) ; and the denominator gets "eliminated";
{since the denominator is equal to "1" ;
& any value (including the numerator), divided by "1" (the denominator),
is equal to that same value (the numerator);
so there is no need for the "denominator".
________________________________________
We can rewrite the equation as:
x = 7 * 8 ; and solve; → 7 * 8 = 56 ;
→ x = 56 .
_____________________________________
Method 3): Given: " 6/7 = 48/x " ; Solve for "x" ;
____________________________________________________
→ 6/7 = 48/x ;
→ Comparing the "numerators" ; " [ 6 * (what value?) = 48 ?] " ??
→ [ (48 ÷ 6 = (what value?) ] ??
→ 48 ÷ 6 = 8 /
→ So: "6/7" = (6*8) / (7*8) = 48/56 = 48/ x ?? ;
→ x = 56 .
_________________________________________