Answer:
C. The vertex is
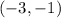 , the domain is all real numbers, and the range is
, the domain is all real numbers, and the range is
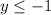 .
.
Explanation:
We have been given a function
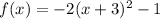 . We are asked to identify the vertex, domain and range of the given function.
. We are asked to identify the vertex, domain and range of the given function.
We can see that our given parabola is in vertex form
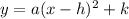 , where
, where
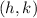 represents vertex of parabola.
represents vertex of parabola.
We can rewrite our given equation as:
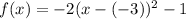
Therefore, the vertex of our given parabola would be
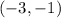 .
.
We know that parabola is a quadratic function and the domain of a quadratic function is all real numbers.
We know that range of a quadratic function in form
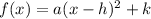 is:
is:
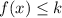 , when
, when
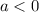 and,
and,
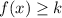 , when
, when
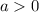
Upon looking at our given function, we can see that
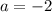 , which is less than 0, therefore, the range of our given function would be
, which is less than 0, therefore, the range of our given function would be
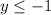 .
.