Answer:
66.667 miles
Explanation:
Given: One car rental company charges $30 per day plus $0.25 per mile driven.
Second car company charges $40 per day plus $0.10 per mile driven.
To find: how many miles must you drive for a one-day rental at the second company to be less expensive than the same rental at the first company?
Solution: Let the distance driven on a day be x miles.
As per question,
The first rental company will charge
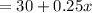
The second rental company will charge
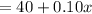
Now, we want the rental charges of second company to be less expensive then the first.
So we get the inequality,
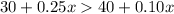
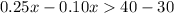
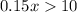
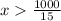
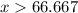 miles
miles
Hence, at least 66.667 miles should be driven on a day.