Question

The sides of an equilateral triangle are increasing at a rate of 10 cm/min. at what rate is the area of the triangle increasing when the sides are 30 cm long?

Answer 1

Area of a triangle is given by


`Area= (1)/(2) ab\sin C= (1)/(2) s^2\sin C`

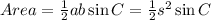
Since the sides of an equilateral triangle are equal.

Differentiating the area of the triangle, we have:


`(dA)/(dt) = (dA)/(ds) \cdot (ds)/(dt) =(s\sin C) (ds)/(dt)`

where


`(ds)/(dt) =10\,cm/min \\ s=30 \, cm`


`\therefore (dA)/(dt) =(30\sin60)*10=300\sin60=259.8\, cm^2/min`

Therefore, the rate is the area of the triangle increasing when the sides are 30 cm long is 259.8 cm^2 / min