To think intuitively of what it means to take a number to a negative power, first consider how we define taking a number to a
positive power.
Before we even get there, though, consider how we define multiplication as
repeated addition. When you see an expression like 3 x 5, what that essentially translates to is "add 3 to itself
5 times," so we could also write 3 x 5 as 3 + 3 + 3 + 3 + 3. Having established that, around middle school, you'll typically get your first exposure to positive exponents, which are defined at first as
repeated multiplication. When you see something like
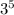
, we could also read that as "multiply 3 by itself
5 times," or
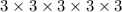
.
With that definition for
positive exponents defined, it makes sense that we would define
negative exponents in terms of the inverse of repeated multiplication: repeated
division. Each time we step the exponent back by 1, we divide by the base again. For example, let's take these decreasing powers of 3 and notice what happens:
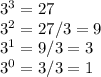
If we start stepping back further, we start getting to values below 1:
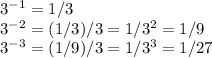
And this pattern continues, with the essential takeaway being that
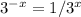
Try applying that pattern to the equation you've been given,
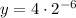
, and see what you get!