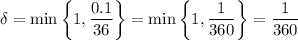Question

Lim x → 2 (x3 − 3x + 3) = 5 illustrate the definition by finding the largest possible values of δ that correspond to ε = 0.2 and ε = 0.1

Answer 1

`\displaystyle\lim_(x\to2)(x^3-3x+3)=5`

is to say that for any
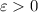
`\varepsilon>0`, we can find
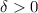
`\delta>0` that guarantees


`|x-2|<\delta\implies|(x^3-3x+3)-5|<\varepsilon`


`|(x^3-3x+3)-5|=|x^3-3x-2|`

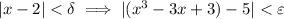
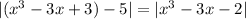
Observing that
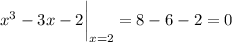
`x^3-3x-2\bigg|_(x=2)=8-6-2=0`, the polynomial remainder theorem tells us that we can factorize the cubic to get


`|x^3-3x-2|=|(x-2)(x^2+2x+1)|=|(x-2)(x+1)^2|=|x-2|(x+1)^2`

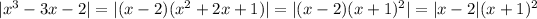
If we assume
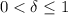
`0<\delta\le1`, we can set up a corresponding upper bound on the quadratic factor. We start with
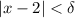
`|x-2|<\delta`, from which we have


`|x-2|<\delta\le1\implies1\le x-2\le3\implies4\le x+1\le6\implies(x+1)^2\le36`

Now,


`|x-2|(x+1)^2<36|x-2|<\varepsilon\implies |x-2|=\frac\varepsilon{36}`

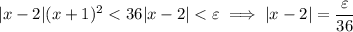
which suggests that we can choose
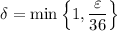
`\delta=\min\left\{1,\frac\varepsilon{36}\right\}` to ensure that we arrive at the inequality
`|(x^3-3x+3)-5|<\varepsilon`.

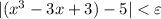
So, given
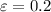
`\varepsilon=0.2`, we would have


`\delta=\min\left\{1,(0.2)/(36)\right\}=\min\left\{1,\frac1{180}\right\}=\frac1{180}`

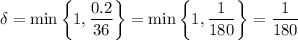
If
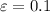
`\varepsilon=0.1`, we would take


`\delta=\min\left\{1,(0.1)/(36)\right\}=\min\left\{1,\frac1{360}\right\}=\frac1{360}`