Question

Find the limit, if it exists, or type dne if it does not exist.

a. \displaystyle\lim_{(x, y) \rightarrow (0, 0)} \frac{(x + 23y)^2}{x^2 + 529y^2} =

Answer 1

`\displaystyle\lim_((x,y)\to(0,0))(\left(x+23y)^2)/(x^2+529y^2)`

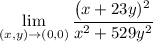
Suppose we choose a path along the
`x`-axis, so that
`y=0`:


`\displaystyle\lim_(x\to0)(x^2)/(x^2)=\lim_(x\to0)1=1`

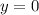
On the other hand, let's consider an arbitrary line through the origin,
`y=kx`:


`\displaystyle\lim_(x\to0)((x+23kx)^2)/(x^2+529(kx)^2)=\lim_(x\to0)((23k+1)^2x^2)/((529k^2+1)x^2)=\lim_(x\to0)((23k+1)^2)/(529k^2+1)=((23k+1)^2)/(529k^2+1)`

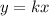
The value of the limit then depends on
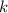
`k`, which means the limit is not the same across all possible paths toward the origin, and so the limit does not exist.