Question

A scientist studying bacteria begins with 20 cells. The bacteria population doubles every hour. Complete the table below to determine after how many hours there will be more than 500 bacteria cells. Time (hours) Number of bacteria cells 0 20 1 40 2 80 3 4 5 6 Write an exponential function to model this situation. Predict the bacteria population after 11 hours.

Answer 1

The bacteria population will be 40,960 in 11 hours

Answer 2

1)

t=5 hours.

2)

40960 cells.

Explanation:

A scientist studying bacteria begins with 20 cells.

The bacteria population doubles every hour.

Let P(t) determines the population of the bacteria in 't' hours.

Hence, by the given information our function P(t) is modeled as:

`P(t)=20* 2^t`

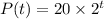
Now, we have to find the value of 't' such that:

P(t)>500

i.e.

`20* 2^t>500\\\\\\2^t>(500)/(20)\\\\2^t>25`

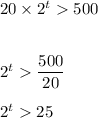
on taking logarithmic function on both side we get:

`t\log 2>\log 25\\\\t>(\log 25)/(\log 2)\\\\t>4.64`

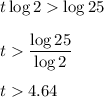
i.e. after 5 hours the population of the bacteria will exceed 500.

Now we have to find the value of function P(t) when t=11.

i.e.

`P(11)=20* 2^(11)\\\\P(11)=20* 2048\\\\P(11)=40960`

Hence , the population of bacteria after 11 hours is:

40960 cells.