Question

A man rides a bicycle a distance of 48 miles in a certain amount of time. If the man increased his speed by 2 miles per hour, he reaches his destination four hours earlier. Find his usual speed. Show Work!

Answer 1

-6 ,4 but speed can't go negative so the answer would be 4.

Answer 2

recall your d = rt, distance = rate * time.

so, in his usual speed, say is hmm "r" mph, so in his usual "r" speed, he rolls on for the 48 miles and it takes him "t" hours to get there.

now, if he increases his speed by 2 mph, then his new speed is "r + 2", and he arrives there 4 hours earlier, so if he took "t" hours going at "r" speed, then when he's going faster at "r + 2", he only takes "t - 4" hours, for the same 48 miles.


`\bf \begin{array}{lccclll} &\stackrel{miles}{distance}&\stackrel{mph}{rate}&\stackrel{hours}{time}\\ &------&------&------\\ \textit{usual speed}&48&r&t\\ \textit{faster speed}&48&r+2&t-4 \end{array} \\\\\\ \begin{cases} 48=rt\implies (48)/(r)=\boxed{t}\\ 48=(r+2)(t-4)\\ ----------\\ 48=(r+2)\left( \boxed{(48)/(r)}-4 \right) \end{cases} \\\\\\ 48=(r+2)\left( \cfrac{48-4r}{r} \right)\implies 48r=(r+2)(48-4r)`


`\bf 48r=48r-4r^2+96-8r\implies 0=-4r^2+96-8r \\\\\\ 4r^2+8r-96=0\implies r^2+2r-24=0 \\\\\\ (r+6)(r-4)=0\implies r= \begin{cases} -6\\ \boxed{4} \end{cases}`

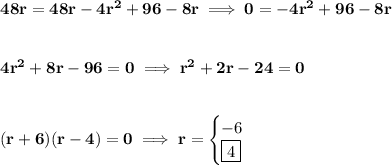
it cannot be a negative value, since is just a forward speed rate, so can't be -6.