Question

The gasoline prices in seven states are $1.96, $2.09, $1.79, $1.61, $1.75, 2.11, and $1.84 what is the median gas price and the difference of the first and third quartiles

Answer 1

first we must put them in order

1.61, [1.75], 1.79, (1.84), 1.96, [2.09], 2.11

the median (the middle number) = 1.84 <=

the difference of the first and 3rd quartiles (the IQR) =
2.09 - 1.75 = 0.34 <=

Answer 2

Median = $1.84

The difference of the first and third quartiles = $0.34

Explanation:

Median

How to calculate the median of a small data or ungrouped data;

1. Arrange the data in ascending or descending order.

2. Choose the middle value. The middle value can be a single value or two value. If the middle value is a single value, then, that value is the median but if the middle values are two, the mean of the two middle values is evaluated to get the median.

Arranging the gasoline prices given in ascending order;

$1.61, $1.75, $1.79, $1.84, $1.96, $2.09, $2.11

The middle value is a single number $1.84 in bold. Therefore, the median is $1.84.

Median = $1.84

First (Lower) Quartile

To calculate for the First (Lower) quartile,

1. Arrange the data give in ascending order.

2. The First (Lower) quartile, Q1 is then calculated using;

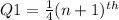`Q1 =(1)/(4) (n + 1)^(th)` term

where n is the total number of terms of the data. In the given question, the total number of terms, n = 7

`Q1 =(1)/(4) (7 + 1)^(th)` term

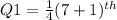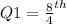`Q1 =(8)/(4)^(th)` term

Q1 = 2nd term

3. Select the 2nd term of the given data already arranged in ascending order.

$1.61, $1.75, $1.79, $1.84, $1.96, $2.09, $2.11

The First Quartile, Q1 = $1.75

Third (Upper) Quartile

To calculate for the third (upper) quartile,

1. Arrange the data give in ascending order.

2. The third (upper) quartile (Q3) is then calculated using;

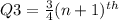`Q3 =(3)/(4) (n + 1)^(th)` term

where n is the total number of terms. In the given question, the total number of terms, n = 7

`Q3 =(3)/(4) (7 + 1)^(th)` term

`Q3 =(24)/(4)^(th)` term

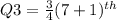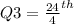`Q3 = 6^(th) term`

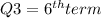
3. Select the
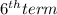`6^(th) term` of the given data already arranged in ascending order.

$1.61, $1.75, $1.79, $1.84, $1.96, $2.09, $2.11

The third (upper) quartile Q3 = $2.09

The difference between the first and third quartiles is called interquartile range.

Now, calculating the difference of the first and third quartiles

Interquartile Range = Q3 - Q1

$2.09 - $1.75 = $0.34

The difference of the first and third quartiles, Interquartile Range = $0.34