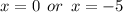Question

Which of the following describes the zeroes of the graph of f(x) = 3x6 + 30x5 + 75x4?

Answer 1

–5 with multiplicity 2 and 0 with multiplicity 4

Explanation:

I just got it wrong on edge 2020

Answer 2

ANSWER

The zeros are:

`x = 0 \: \: or \: \: x = - 5`
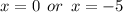
with multiplicity of 4 and 2 respectively.


EXPLANATION

The given function is


`f(x) =3 {x}^(6) + 30 {x}^(5) + 75 {x}^(4)`
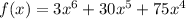
We want to find


`3 {x}^(6) + 30 {x}^(5) + 75 {x}^(4) = 0`

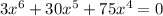
We can find the zeros of this function by factorizing the greatest common factor to obtain,


`3 {x}^(4) ( {x}^(2) + 10x + 25) = 0`

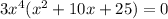
The expression in the bracket can be rewritten as,


`3 {x}^(4) ( {x}^(2) + 2(5)x + {5}^(2) ) = 0`

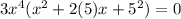
We can see clearly that, the expression in the bracket is a perfect square that can be factored as,


`3 {x}^(4) ( x+ 5)^2 = 0`

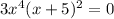
This implies that,


`3 {x}^(4) = 0`
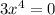
or


`(x + 5) ^(2) = 0`

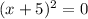
This gives,


`{x}^(4) = 0 \: \: or \: \: x + 5 = 0`

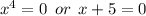
This finally gives,


`x = 0 \: \: or \: \: x = - 5`