Determine the interval on which f(x) = the square root of the quantity of x plus 2 is integrable. (−∞, 2) [−2, ∞) (−∞,−2) U (−2, ∞) All reals

Question

asked Oct 5, 2018 209k views

1 Answer

Noy Oliel · Answer 1 · 2018-10-09T01:43:35+0000

The interval on which f(x) is integrable is:

[-2, ∞)

We are given a function f(x) as:

f(x)=√(x+2)

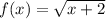
We know that a function is integrable over a given interval if it is continuous over a given interval.

Now, we know that the square root function is well defined if the function under the square root sign is positive.

This means here the function is well defined if:

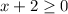
$x+2\geq 0$

i.e.

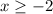
$x\geq -2$

Also, the square root function is continuous over it's domain.

and hence it is integrable over it's domain.

This means that the function is integrable over:

[-2,∞)