Question

Suppose △ABC≅△EFG. Which congruency statement is true? AB¯¯¯¯¯≅FG¯¯¯¯¯ BC¯¯¯¯¯≅FG¯¯¯¯¯ AC¯¯¯¯¯≅EF¯¯¯¯¯ AB¯¯¯¯¯≅EG¯¯¯¯¯

Answer 1

A = E

B = F

C = G

Look for the equation which has the same placement. Your answer should be B) BC=FG

Answer 2

Answer: Second option
`BC\cong FG` is the correct option.

Step-by-step explanation:

If two triangles are congruent then their corresponding sides are congruent.

In
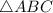`\triangle ABC` and
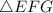`\triangle EFG`, AB, BC, and CA are corresponding to EF, FG and GE respectively.

Therefore, if
`\triangle ABC\cong \triangle EFG` then,

`AB\cong EF`,

`BC\cong FG`,

And,
`CA\cong GE`

Therefore, only second option is correct.