Question

To the nearest tenth, find the perimeter of ∆ABC with vertices A(2,4), B(-2,1) and C(2,1). Show your work.

Answer 1

First, we should calculate the lengths of the three sides (see the figure below).

The distance between two coordinates (x₁, y₁) and (x₂, y₂) is given by the formula

`d= \sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)}`

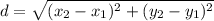
Because the triangle is a right angle (indicated by the figure), we can determine the lengths of BC and AC easily.
The length of BC is the change in the x-coordinates, and AC is the change in the y-coordinates.
BC = 2 - (-2) = 4
AC = 4 - 1 = 3

To find AB, use the distance formula (the same as the Pythagorean theorem).
AB = √[(2-(2)) ²+ (4-1)² ] = √(4²+3²) = √25 = 5

The area of the triangle is (1/2)*BC*AC = (1/2)*4*3 = 6

Answer: 6