Question

A small rocket is launched vertically, attaining a maximum speed at burnout of 1.0 ✕ 10^2 m/s and thereafter coasting straight up to a maximum altitude of 1494 m. Assuming the rocket accelerated uniformly while the engine was on, how long did it fire and how high was it at engine cut off

Answer 1

The distance traveled and time taken by the rocket are 1488.89 m and 14.8 sec.

Step-by-step explanation:

Given that,

Initial velocity
`u= 1.0*10^2\ m/s`

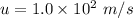
Altitude = 1494 m

We need to calculate the distance

Using equation of motion

`v^2=u^2+2as`

Where, v = final velocity

u = initial velocity

a = acceleration due to gravity

s = distance

Put the value into the formula

`0=(1.0*10^2)^2+2*(-9.8)* s`

`s=(1.0*10^(2))/(2*9.8)`

`s=5.10204\ m`

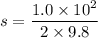
So, The distance from the start of the coast to the end is 5.10204 m

The distance traveled by the rocket

`1494-5.10204=1488.89\ m`

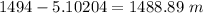
We need to calculate the time

Using formula of time

`t=(d)/(v)`

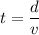
Where, v = speed

t = time

d = distance

Put the value into the formula

`t=(1488.89)/(1.0*10^(2))`

`t=14.8\ sec`

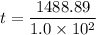
Hence, The distance traveled and time taken by the rocket are 1488.89 m and 14.8 sec.

Answer 2

The first thing we can compute for is the altitude the rocket was at engine cutoff using the formula:

v^2 = v0^2 + 2ad

where v = final velocity = 0, v0 = 1 x 10^2 m/s, a = -9.8 m/s^2, so d is:

- (1 x 10^2 m/s)^2 = 2 * (-9.8 m/s^2) * d

d = 1,020.41 m

Then finding for the time using the formula:

2d = (v – v0) * t

where d = 1020.41 m, v0 = 0, v = 1 x 10^2 m/s

t = 2 * 1020.41 m / 1 x 10^2 m/s

t = 20.41 seconds