Question

Determine the exact values of the six trigonometric functions of the real number t

Answer 1

`\bf sin(\theta)=\cfrac{opposite}{hypotenuse} \qquad\qquad \qquad cos(\theta)=\cfrac{adjacent}{hypotenuse}\\\\ -------------------------------\\\\ \textit{the point on the graph is }\left( \stackrel{cosine}{-\cfrac{8}{17}}~,~\stackrel{sine}{\cfrac{15}{17}} \right)`

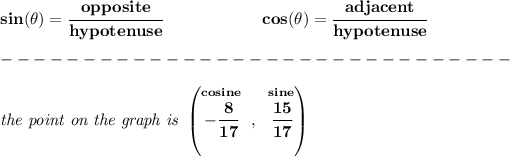
now, keep in mind that, the hypotenuse is just the radius unit, so is never negative, so if the cosine is negative, that simply means it has to be the numerator, the 8 is negative, -8. that means


`\bf cos(\theta )=\cfrac{\stackrel{adjacent}{-8}}{\stackrel{hypotenuse}{17}}\qquad \qquad sin(\theta )=\cfrac{\stackrel{opposite}{15}}{\stackrel{hypotenuse}{17}}`


so, the adjacent is -8, the opposite side is 15, and the hypotenuse is 17, so just plug them in then


`\bf sin(\theta)=\cfrac{opposite}{hypotenuse} \qquad cos(\theta)=\cfrac{adjacent}{hypotenuse} \quad % tangent tan(\theta)=\cfrac{opposite}{adjacent} \\\\\\ % cotangent cot(\theta)=\cfrac{adjacent}{opposite} \quad % cosecant csc(\theta)=\cfrac{hypotenuse}{opposite} \qquad % secant sec(\theta)=\cfrac{hypotenuse}{adjacent}`