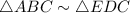Question

Question 1 (Worth 4 points)

(02.07)The figure shows two parallel lines AB and DE cut by the transversals AE and BD:

AB and DE are parallel lines, and AE and BD are transversals. The transversals intersect at C. Angle CAB is labeled 1, angle ABC is labeled 2, angle ACB is labeled 3, angle ACE is labeled 4, angle CDE is labeled 6, and angle CED is labeled 5.

Which statement best explains the relationship between Triangle ABC and Triangle EDC ?

Triangle ABC is similar to triangle EDC , because m∠2 = m∠6 and m∠1 = m∠5

Triangle ABC is similar to triangle EDC , because m∠3 = m∠6 and m∠1 = m∠4

Triangle ABC is congruent to triangle EDC , because m∠3 = m∠4 and m∠1 = m∠5

Triangle ABC is congruent to triangle EDC , because m∠3 = m∠6 and m∠1 = m∠4

Points earned on this question: 4

Answer 1

Explanation:

Answer 2

Answer: 'Triangle ABC is similar to triangle EDC , because
`m\angle 2=m\angle 6` and
`m\angle 1=m\angle 5`

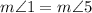
' is the correct option.

Step-by-step explanation:

Since, Here
`AB\parallel DE` and BD and AE are the transversals which cut these two parallel lines

Thus according to the figure,
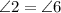`\angle 2= \angle 6` ( Because alternative interior angles made by the same transversal on two parallel lines are always equal)

Similarly,
`\angle 1=\angle 5`

Thus In triangles ABC and DCE,

`\angle 2= \angle 6`

And,
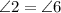
`\angle 1=\angle 5`

thus If In two triangles two corresponding angles are equal, then they are similar to each other.

Therefore,
`\triangle ABC\sim \triangle EDC`