Question

Determine if the inverse of function {(-3, -6), (-1, 2), (1, 2), (3, 6)} is also a function.

Answer 1

well... for an equation to be a function, its domain must be unique, namely, the x-coordinate values in the coordinate pairs must not have any repeats.

so... first off, let's check this pairs for this expression.


`\bf \{(\stackrel{\downarrow }{-3}, -6), (\stackrel{\downarrow }{-1}, 2), (\stackrel{\downarrow }{1}, 2), (\stackrel{\downarrow }{3}, 6)\} \impliedby \textit{so, that's the domain for f(x)}`

notice, is just -3, -1, 1 and 3... no x-values repeat, all are different, so it IS indeed a function.

now... a distinct issue of an inverse function is that, its domain is the range of the original function, to make it short and simple, the value pairs for the inverse of this function is simply the same value pairs flipped sideways, well, let's check the domain of the inverse then.


`\bf \{(-6,-3), (2,-1), (2,1), (6,3)\}\impliedby \textit{value pairs for }f^(-1)(x) \\\\\\ \textit{let's check its domain}\quad \{(\stackrel{\downarrow }{-6},-3), (\stackrel{\stackrel{re peat}{\downarrow }}{2},-1), (\stackrel{\stackrel{re peat}{\downarrow }}{2},1), (\stackrel{\downarrow }{6},3)\}`

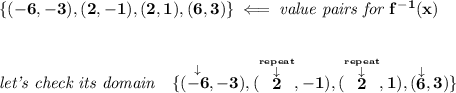
well, there you have it.