Answer: Choice D.
Morgan forgot to distribute the negative sign to two of the terms in the second expression.
=============================================================
Step-by-step explanation:
Focus on the numerators.
We have (3t^2-4t+1) as the first numerator and we subtract off (t^2+2t+2) as the second numerator.
Morgan needs to simplify (3t^2-4t+1)-(t^2+2t+2) for the numerator.
Mistakenly, she had these steps
(3t^2-4t+1)-(t^2+2t+2)
3t^2-4t+1-t^2+2t+2 .... her mistake made here
(3t^2-t^2)+(-4t+2t)+(1+2)
2t^2-2t+3
All of this applies to the numerator. The denominator stays at t+3 the entire time. So effectively we can ignore it on a temporary basis.
Here's what Morgan should have for her steps when simplifying the numerator.
(3t^2-4t+1)-(t^2+2t+2)
3t^2-4t+1-t^2-2t-2 ..... distribute the negative
(3t^2-t^2)+(-4t-2t)+(1-2)
2t^2-6t-1
Note in the second step, the negative outside flips the sign of each term in the second parenthesis.
Therefore,
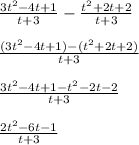
which means
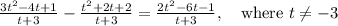
Side notes:
- The fractions can only be subtracted since the denominators are the same.
- We have
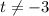 to avoid a division by zero error.
to avoid a division by zero error. - Rational expressions are a fraction, or ratio, of two polynomials.