Answer: The answer is 3 : 4.
Step-by-step explanation: Given that the two similar hexagons have areas of 36 square units and 64 square units. We are to find the ratio of the corresponding sides of the hexagons.
We know that the area of a regular hexagon with side of length 'a' units is given by
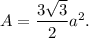
Let, A and B be the areas of the two hexagons and 'a' and 'b' be the lengths of the corresponding sides. Then, we have

According to the question,
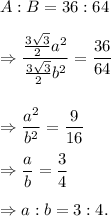
Thus, the required ratio is 3 : 4.