Question

Solve the inequality. 2(4x – 3) ≥ –3(3x) + 5x? x ≥ 0.5 x ≥ 2 (–∞, 0.5]

Answer 1

2(4x - 3) > = -3(3x) + 5x
8x - 6 > = -9x + 5x
8x - 6 > = - 4x
-6 > = -4x - 8x
-6 > = - 12x
-6/-12 < = x
0.5 < = x or x > = 0.5 <==

** if u multiply/divide by a negative, the inequality sign changes

Answer 2

`x\geq 0.5`

Explanation:

Given the inequality:

`2(4x-3)\geq -3(3x)+5x`

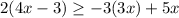
Applying the distributive property on the left hand side :
`a(b-c)=a\cdot b - a\cdot c`

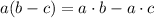
we have then;

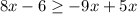`8x-6\geq -9x+5x` or

`8x-6\geq -4x`

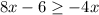
then, following steps to be followed as:

1) Group variable terms on the left side of the inequality

2) Group constant terms on the right side of the inequality

3) Add the variable terms

4) Add the constant terms , then

5) find the value of x

add 6 on both sides we get,

`8x-6+6\geq -4x+6`

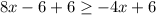
Simplify:

`8x \geq -4x+6`

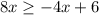
Add 4x on both sides we get,

`8x+4x\geq-4x+6+4x`

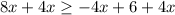
On simplify we get,

`12x\geq 6`

⇒
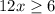
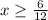`x\geq (6)/(12)` or
`x\geq 0.5`