Question

A number greater than 1000 who is prime factorization contains one prime number that does not repeat one prime number that repeat three times and one prime number that repeats twice

Answer 1

Let the prime number which does not repeat be a, the prime number which repeats twice be b, the prime number which repeats 3 times be c.

Then the prime factorization of this number is
`a\cdot b^2 \cdot c^3`.



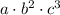
Let's find the prime factorization of 1000:


`1000=10^3=(2 \cdot5)^3=2^3 \cdot5^3`


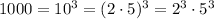
So let c= 5, b be a number such that b^2>2^3=8, for example let b = 3, and let a be any prime, for example 2


thus the number is
`a\cdot b^2 \cdot c^3=2\cdot 3^2 \cdot 5^3=2 \cdot 9 \cdot 125=9 \dot 250=2250`


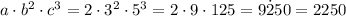
Answer: 2250