Question

Which statement proves that parallelogram KLMN is a rhombus?

A. The midpoint of both diagonals is (4, 4).
B. The length of KM is √72 and the length of NL is √8.
C. The slopes of LM and KN are both 1/2 and NK = ML = √20 .
D. The slope of KM is 1 and the slope of NL is –1.

Answer 1

Answer: D is the right answer.The slope of KM is 1 and the slope of NL is –1.

Explanation:

A rhombus is a parallelogram whose all sides are equal. Its diagonals perpendicularly bisect each other.

i.e. product of its slope should be -1.

[∵if one line is perpendicular to the other lines then product of its slope should be -1.]

In diagram

Slope of KM=
`(7-1)/(7-1)=(6)/(6)=1`

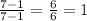
Slope of NL=
`(5-3)/(3-5)=(2)/(-2)=-1`

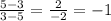
Product of slope of diagonals=1×-1=-1

∴diagonals of given parallelogram perpendicularly bisect each other.

Therefore,it is a rhombus.