Question

Find the absolute maximum and minimum values of the function f(x, y) = x2 + xy + y2 on the disc x2 + y2 ≤ 1

Answer 1

`f(x,y)=x^2+xy+y^2`

`(\partial f)/(\partial x)=2x+y`

`(\partial f)/(\partial y)=2y+x`

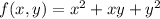
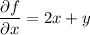
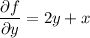
Critical points occur when both partial derivatives vanish; this happens when


`\begin{cases}2x+y=0\\2y+x=0\end{cases}\implies x=0,y=0`

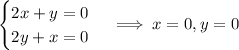
The function has Hessian


`\mathbf H(x,y)=\begin{bmatrix}(\partial^2f)/(\partial x^2)&(\partial^2f)/(\partial x\partial y)\\\\(\partial^2f)/(\partial y\partial x)&(\partial^2f)/(\partial y^2)\end{bmatrix}=\begin{bmatrix}2&1\\1&2\end{bmatrix}`

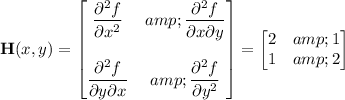
which at
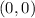
`(0,0)` has
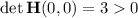
`\det\mathbf H(0,0)=3>0`. And since
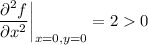
`(\partial^2f)/(\partial x^2)\bigg|_(x=0,y=0)=2>0`, it follows that a local minimum occurs at
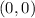
`(0,0)` with a value of
`f(0,0)=0`.

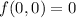
Meanwhile, we can parameterize the boundary by


`\begin{cases}x=\cos t\\y=\sin t\end{cases}`

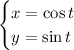
with
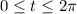
`0\le t\le2\pi`. So


`f(x,y)=f(x(t),y(t))=F(t)=\cos^2t+\sin t\cos t+\sin^2t=1+\frac12\sin2t`

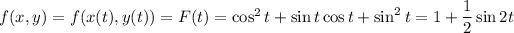
which has critical points when
`F'(t)=0`:


`F'(t)=\cos2t=0\implies 2t=\frac\pi2+n\pi\implies t=\frac\pi4+\frac{n\pi}2`

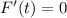
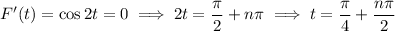
We only have 4 points to worry about:
`t=\frac\pi4,\frac{3\pi}4,\frac{5\pi}4,\frac{7\pi}4`

Now,


`F\left(\frac\pi4\right)=\frac32`

`F\left(\frac{3\pi}4\right)=\frac12`

`F\left(\frac{5\pi}4\right)=\frac32`

`F\left(\frac{7\pi}4\right)=\frac12`

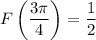
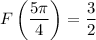
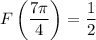
So we find that an absolute minimum occurs at
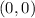
`(0,0)` with a value of
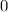
`0`, and two more extrema occur along the boundary when
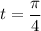
`t=\frac\pi4` and
`t=\frac{5\pi}4`, i.e at the points
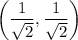
`\left(\frac1{\sqrt2},\frac1{\sqrt2}\right)` and
`\left(-\frac1{\sqrt2},-\frac1{\sqrt2}\right)`, both with the same maximum value of
`\frac32`.