Question

The quantity demanded of a certain brand of DVD player is 3000/wk when the unit price is $485. For each decrease in unit price of $40 below $485, the quantity demanded increases by 500 units. The suppliers will not market any DVD players if the unit price is $334 or lower. But at a unit price of $559, they are willing to make available 2500 units in the market. The supply equation is also known to be linear.

Answer 1

Given that the quantity demanded of a certain brand of DVD player is 3000/wk when the unit price is $485. For each decrease in unit price of $40 below $485, the quantity demanded increases by 500 units. The suppliers will not market any DVD players if the unit price is $334 or lower. But at a unit price of $559, they are willing to make available 2500 units in the market. The supply equation is also known to be linear.

Part (a): Find the demand equation.
To find the demand equation, we notice that the demand function is linear because we were told that for each decrease in unit price of $40 below $485, the quantity demanded increases by 500 units.

Given that at a price of $485, the quantity demanded is 3,000 and given that for each decrease in unit price of $40 below $485, the quantity demanded increases by 500 units. Then for a price of $485 - $40 = $445, the quantity demanded is 3,000 + 500 = 3,500 units

Thus, using the formula for the equation of a straight line and the points (3,000, 485) and (3,500, 445), we find the demand equation as follows:


`(p-485)/(q-3,000) = (445-485)/(3,500-3,000) \\ \\ \Rightarrow (p-485)/(q-3,000)= (-40)/(500) =- (2)/(25) \\ \\ \Rightarrow25(p-485)=-2(q-3,000) \\ \\ \Rightarrow25p-12,125=-2q+6,000 \\ \\ \Rightarrow25p+2q=18,125`



Part (b): Find the supply equation.
To find the supply equation, given that the supply function is linear and that the suppliers will not market any DVD players if the unit price is $334 or lower. But at a unit price of $559, they are willing to make available 2500 units in the market.

Thus, using the formula for the equation of a straight line and the points (0, 334) and (2,500, 559), we find the demand equation as follows:


`(p-334)/(q-0) = (559-334)/(2,500-0) \\ \\ \Rightarrow (p-334)/(q)= (225)/(2,500) =(9)/(100) \\ \\ \Rightarrow100(p-334)=9q \\ \\ \Rightarrow100p-33,400=9q \\ \\ \Rightarrow100p-9q=33,400`



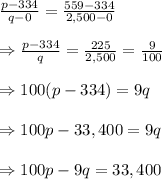
(c) Find the equilibrium quantity and price.
The equilibruim quantity and price is given by the quantity and price at which the quantity demanded is equal to the quantity supplied. It is obtained by equating the demand and the supply equations.

i.e.
From demand equation, we have

`25p+2q=18,125 \\ \\ \Rightarrow25p=-2q+18,125 \\ \\ \Rightarrow p= -(2)/(25)q +725 \ . \ . \ . (1)`

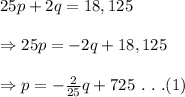
From supply equation, we have

`100p-9q=33,400 \\ \\ \Rightarrow100p=9q+33,400 \\ \\ \Rightarrow p= (9)/(100) q+334 \ . \ . \ . (2)`

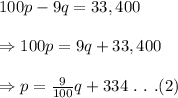
Equating equations (1) and (2), we have

`-(2)/(25)q +725=(9)/(100) q+334 \\ \\ \Rightarrow(9)/(100) q+(2)/(25)q=725-334 \\ \\ \Rightarrow (17)/(100) q=391 \\ \\ \Rightarrow q= (391*100)/(17) =2,300`

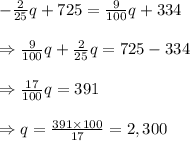
Substituting for q into equation (1), we have

`-(2)/(25)(2,300) +725=-184+725=541`

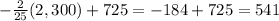
Therefore, the equilibruim quantity is 2,300 units at a price of $541.