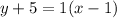Question

Write the point-slope form of the line that passes through (1, -5) and is parallel to a line with a slope of 1. Include all of your work in your final answer. Type your answer in the box provided or use the upload option to submit your solution.

Answer 1

y - y1 = m(x - x1)
slope(m) = 1...because a parallel line will have the same slope
(1,-5)...x1 = 1 and y1 = -5
now we sub
y - (-5) = 1(x - 1) =
y + 5 = 1(x - 1) <== u could leave that first " one " out if u want...

Answer 2

`y+5=1(x-1)`

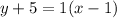
Explanation:

The point-slope form of a line is:

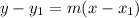`y-y_(1)=m(x-x_(1))`; where
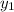`y_(1)` and
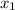`x_(1)` are the coordinates of a given point, and m is the slope.

In addition, when two line are parallel means that they both have the same slope. So, the point-slope form we have to find it's gonna have
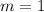`m=1`, because is parallel to a line with that slope. Also, the given point is
`(1;-5)`.

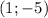Now, we just replace all values and isolate
`y`:

`y_(2)-y=m(x_(2)-x)\\y-(-5)=1(x-1)\\y+5=1x-1\\y=1x-1-5\\y=x-6`

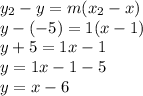
Therefore, the equation of the parallel line is:

`y=x-6`

And the point-slope form is:

`y+5=1(x-1)`