Let the least possible value of the smallest of 99 cosecutive integers be x and let the number whose cube is the sum be p, then
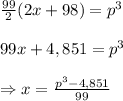
By substitution, we have that
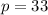
and
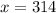
.
Therefore,
the least possible value of the smallest of 99 consecutive positive integers whose sum is a perfect cube is 314.