Notice that the difference between 2 consecutive terms is 6,
Let
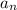
mean the n'th term of the sequence, so:
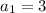
,

,
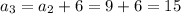
The sequence is "arithmetic" means that every term, is its previous term + 6, the common difference.
So the sequence is 3, 9, 15, 21, 27, ....
write again each term of the sequence to see how we get it, so that we are able to figure out a general formula:
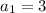
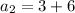
![a_3=[3+6]+6](https://img.qammunity.org/2018/formulas/mathematics/high-school/tnmuo728bwypw1lyiu4yqekdidaut11zww.png)
![a_4=[3+6+6]+6](https://img.qammunity.org/2018/formulas/mathematics/high-school/abqp02whprk4ohyni2x84js5aslqwa6a21.png)
![a_5=[3+6+6+6]+6](https://img.qammunity.org/2018/formulas/mathematics/high-school/waiw6li8eajuwl1g0thn5x6477wvw3fnvc.png)
.
.
so we notice that to find the 6.th term we need to add 5 sixes to 3.
to find the 7.th term we add 6 sixes to 3,
In general, to find the n.th term, we add (n-1) sixes to 3
Thus, the general formula is
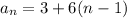
,
The sum of the first 34 terms of the sequence is

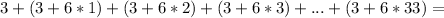
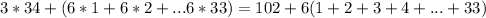
the sum of the first A consecutive numbers 1+2+3+4+...+A is equal to :
A(A+1)/2 , according to the famous Gauss formula,
so 1+2+3+...+33= 33(33+1)/2=(33*34)/2=17*33=561
Thus, 102+6(1+2+3+4+...+33)= 102+6*561=102+ 3366=3,468
Answer: D) 3,468