A geometric series is the sum of the terms of a geometric sequence of the form
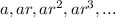
,
where r is the common ratio, and a≠0 is the first term.
That is, the series is
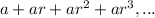
In sigma notation, the series is written as:
∞
∑
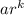
k=0
--------------------------------------------------------------------------------------------------
The geometric series of the form
∞
∑
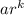
, converges to
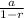
if |r|<1
k=0
and diverges otherwise.
--------------------------------------------------------------------------------------------------
in our problem, a , the first term is equal to 940, and the common ratio is |1/5|<1,
thus the series converges to:
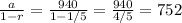
Answer:
∞
∑

=752 ( the upper limit of the population is 752)
k=0