Question

Estimate square root of 15 to the nearest tenth then locate square root 15 on a number line

Answer 1

Newton's numerical method to estimate the square root of N uses the iterative relation

`x_(n+1) = (1)/(2) (x_(n) + (N)/(x_(n))), \, for \, n=0,1,2, \, ...,`
x₀ = initial guess

We want to estimate the square root of 15, so N = 15.
We know that √{16) = 4, therefore let x₀ = 4 for the initial guess.

Calculate relative error after n iterations as

`e_(n) = |1 - (x_(n))/(x_(n+1)) |`
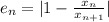
When the relative error is less than 0.01, we shall accept the approxmate answer.

Iteration #1:
x₁ = 0.5(x₀ + N/x₀) = 0.5(4 + 15/4) = 3.875
e₁ = |1 - 4/3.875| = 0.032

Iteration #2:
x₂ = 0.5(3.875 + 15/3.875) = 3.873
e₂ = |1 - 3.875/3.873| = 5.2 x 10⁻⁴
This is good enough.

Therefore the approximate value for √(15) is 3.873.
On a number line, the progression to find the square root is shown below.

Answer: 3.873