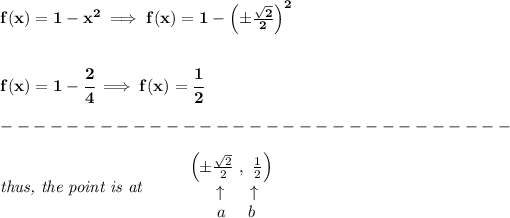Question

Find the poin on the graph of f(x)=1-x^2 that are closest to0(0,0)

Answer 1

we know the graph goes through the point 0,0, and we also know the graph goes through say, another point, say x,y, and the point x,y lies on the graph of f(x), check the left-side of the picture below.

now.... what is the length of that line? well, let's use the distance formula for that.





`\bf l=\left[ \boxed{x^2}~+~\left( \boxed{1-x^2} \right)^2\right]^{(1)/(2)}\implies l=(x^2+1-2x^2+x^4)^{(1)/(2)} \\\\\\ l(x)=(x^4-x^2+1)^{(1)/(2)}\\\\ -------------------------------\\\\ \cfrac{dl}{dx}=\cfrac{1}{2}(x^4-x^2+1)^{-(1)/(2)}(4x^3-2x)\implies \cfrac{dl}{dx}=\cfrac{4x^3-2x}{2√(x^4-x^2+1)} \\\\\\ \cfrac{dl}{dx}=\cfrac{2x^3-x}{√(x^4-x^2+1)}`

now, let's set the derivative of that "length" equation to 0, to check the critical points, now, we also do get critical points when the denominator is 0, however, in this case, it doesn't yield any.


`\bf 0=x(2x^2-1)\implies \begin{cases} 0=x\\ ------\\ 0=2x^2-1\\ (1)/(2)=x^2\\ \pm (√(2))/(2)=x \end{cases}`

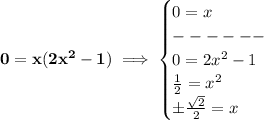
so.. .if we check the regions on those critical points, doing a first-derivative test, check the picture's right-side, we get that
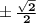
`\bf \pm (√(2))/(2)` are indeed minima, and so, what's "y" when "x" is that? well


`\bf f(x)=1-x^2\implies f(x)=1-\left( \pm(√(2))/(2) \right)^2\\\\\\ f(x)=1-\cfrac{2}{4}\implies f(x)=\cfrac{1}{2}\\\\ -------------------------------\\\\ \textit{thus, the point is at }\qquad \begin{array}{llll} \left(\pm(√(2))/(2)~,~(1)/(2) \right)\\ ~~~~\uparrow~~~\uparrow \\ ~~~~~a~~~~b \end{array}`