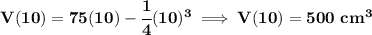If 300cm^(2)300 cm of material is available to make a box with a square base and an open top, find the maximum volume of the box in cubic centimeters. Answer to the nearest cubi…

Question

If
`300cm^(2)`300 cm of material is available to make a box with a square base and an open top, find the maximum volume of the box in cubic centimeters. Answer to the nearest cubic centimeter without commas. For example, if the answer is 2,000 write 2000.

Answer 1

check the picture below. Recall, is an open-top box, so, the top is not part of the surface area, of the 300 cm². Also, recall, the base is a square, thus, length = width = x.


`\bf \textit{volume of a rectangular prism}\\\\ V=lwh\quad \begin{cases} l = length\\ w=width\\ h=height\\ -----\\ w=l=x \end{cases}\implies V=xxh\implies \boxed{V=x^2h}\\\\ -------------------------------\\\\ \textit{surface area}\\\\ S=4xh+x^2\implies 300=4xh+x^2\implies \cfrac{300-x^2}{4x}=h \\\\\\ \boxed{\cfrac{75}{x}-\cfrac{x}{4}=h}\\\\ -------------------------------\\\\ V=x^2\left( \cfrac{75}{x}-\cfrac{x}{4} \right)\implies V(x)=75x-\cfrac{1}{4}x^3`

so.. that'd be the V(x) for such box, now, where is the maximum point at?


`\bf V(x)=75x-\cfrac{1}{4}x^3\implies \cfrac{dV}{dx}=75-\cfrac{3}{4}x^2\implies 0=75-\cfrac{3}{4}x^2 \\\\\\ \cfrac{3}{4}x^2=75\implies 3x^2=300\implies x^2=\cfrac{300}{3}\implies x^2=100 \\\\\\ x=\pm10\impliedby \textit{is a length unit, so we can dismiss -10}\qquad \boxed{x=10}`

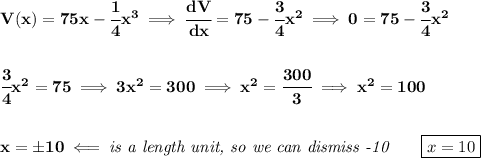
now, let's check if it's a maximum point at 10, by doing a first-derivative test on it. Check the second picture below.

so, the volume will then be at
`\bf V(10)=75(10)-\cfrac{1}{4}(10)^3\implies V(10)=500 \ cm^3`