Question

Express the complex number in trigonometric form. -6 + 6 square root of 3 i ?

Answer 1

`\bf \begin{array}{clclll} -6&+&6√(3)\ i\\ \uparrow &&\uparrow \\ a&&b \end{array}\qquad \begin{cases} r=√(a^2+b^2)\\ \theta =tan^(-1)\left( (b)/(a) \right) \end{cases}\qquad r[cos(\theta )+i\ sin(\theta )]\\\\ -------------------------------\\\\`


`\bf r=\sqrt{(-6)^2+(6√(3))^2}\implies r=√(36+(6^2\cdot 3))\implies r=√(144) \\\\\\ r=12\leftarrow \\\\\\ \theta =tan^(-1)\left( (6√(3))/(-6) \right)\implies \theta =tan^(-1)\left( -√(3)\right)\implies \theta = \begin{cases} (2\pi )/(3)\leftarrow \\ (5\pi )/(3) \end{cases}`

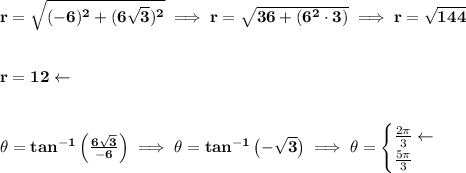
now, notice, there are two valid angles for such a tangent, however, if we look at the complex pair, the "a" is negative and the "b" is positive, that means, "x" is negative and "y" is positive, and that only occurs in the 2nd quadrant, so the angle is in the second quadrant, not on the fourth quadrant.

thus
`\bf 12\left[cos\left( (2\pi )/(3) \right) +i\ sin\left( (2\pi )/(3) \right) \right]`