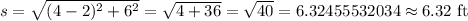Question

The lower base of the frustum shown in the figure is a square 8 ft on each side. The upper base is a square 4 ft on each side. If the altitude is 6 ft, find the slant height

Answer 1

The answer to this question is:

The lower base of the frustum shown in the figure is a square 8 ft on each side. The upper base is a square 4 ft on each side. If the altitude is 6 ft, find the slant height"6.32 ft"

Hope This Helped, Olikjyhtgrfedwsqa
Your Welcome:)

Answer 2

The slant height is 6.32 ft ( approx )

Explanation:

Since, the slant height formula of a square frustum,

`s=√((r_1-r_2)^2+h^2)`

Where,
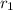`r_1` is apothem of the lower base,

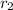`r_2` is the apothem of the upper base,

And, h is the altitude,

Given,

The lower base is a square 8 ft on each side,

So, its apothem,

`r_1=(8)/(2tan((180)/(4)))=(4)/(tan45)=4`

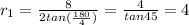
Similarly,

The upper base is a square 4 ft on each side,

`\implies r_2=(4)/(2tan((180)/(4)))=2`

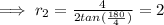
Also, h = 6 ft,

Hence, the slant height of the given frustum is,

`s=√((4-2)^2+6^2)=√(4+36)= √(40)=6.32455532034\approx 6.32\text{ ft}`