Question

a student's work to distribute and simplify a radical is shown below. Select the statement which best applies to the sample mathematical work. given (-5√20+√3)*(2+√3), i first distribute to get the expression -10√20-5√60+2√3+√9, which i can simplify to -40√5-20√15+2√3+3 for an answer. a. the student did not properly distribute the radicals b. the student overlooked combining one or more of the radical terms c. the student did not properly simplify all radicals d. the work shown above is correct

Answer 1

`(-5 √(20) + √(3) )(2+ √(3) )\\ \\ -10 √(20)-5 √(60) +2 √(3)+ √(9) \\ \\ -20 √(5)-10 √(15)+2 √(3)+3`


Answer is c. the student did not properly simplify all radicals.
[5√60 = 10√15, not 20√15]

Answer 2

C) The student did not properly simplify all radicals.

Explanation:

We are given the following expression in the question:

`(-5√(20)+√(3))(2+√(3))`

We have to apply the distributive property.

Distributive Property:

• The distributive property helps multiply a sum by multiplying each addend separately and then add the products.

• (a+b)(c+d) = ac + ad + bc + bd

Applying the distributive property:

`(-5√(20)+√(3))(2+√(3))\\(-5√(20))(2) + (-5√(20))(\sqrt3) + (\sqrt3)(2) + (\sqrt3)(\sqrt3)\\-10√(20)-5√(60)+2\sqrt3 +\sqrt9`

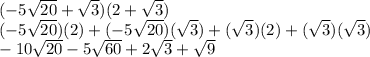
This can be further simplified as:

`-10√(20)-5√(60)+2\sqrt3+\sqrt9\\-20√(5)-10√(15)+2\sqrt3+3`

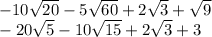
The student simplified the radical as:

`-40√(20)-20√(60)+2\sqrt3+\sqrt3`

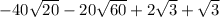
The student did a mistake in simplifying the radical. He did not solve the square roots properly.

C) The student did not properly simplify all radicals.