Question

AB=diameter of the circle O. OC=radius. Arc AXB is an arc of the circle with centre C. Prove areas of the shaded region are =

Answer 1

1.
Draw a circle with center C And radius CA, as shown in the attached picture.

Let the lengths of radii AO, OB, OC be R. Triangle ABC is inscribed in the circle with center O and one of its sides is a diameter, this means that the angle ACB is a right angle.
|AO|=|OC|=R, by the Pythagorean theorem |AC|=
`√(2)R`.

these are all shown in the picture.

2.

Area of triangle ABC is 1/2 * 2R * R= R^2

3.

Let the area between arc BXA and chord AB be Y. (the yellow region).

and let G be the shaded region between arcs AB and AXB.

G=1/2(Area circle with center O)-Y
=
`(1)/(2) \pi R^(2)-Y`

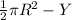
To find Y:

Notice that the area of the sector ACB is 1/4 of the area of circle with center C, since m(ACB) is 1/4 of 360 degrees.

So Area of sector ACB =
`(1)/(4) \pi (√(2) R)^(2)=(1)/(4) \pi*2 R^(2) =(1)/(2) \pi R^(2)`

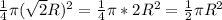
Y =area of sector ABC-Area(triangle ABC)=
`(1)/(2) \pi R^(2)- (1)/(2)*2R*R=(1)/(2) \pi R^(2)- R^(2)`


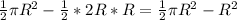
4.

Finally,


`G=(1)/(2) \pi R^(2)-Y=(1)/(2) \pi R^(2)-((1)/(2) \pi R^(2)- R^(2))=R^(2)`

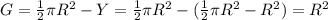
This proves that the 2 shaded regions have equal area.