Question

A cone shaped funnel has a radius of 3 inches and a height of 7 inches.

Betty closes the nozzle of the funnel and fills it completely with a liquid. She then opens the nozzle. If the liquid drips at the rate of 14 cubic inches per minute, how long will it take for all the liquid in the funnel to pass through the nozzle? (Use π = 3.14.)

A) 4.71 minutes


B) 3.14 minutes


C) 14.13 minutes


D) 9.42 minutes

Answer 1

V=Pi*r^2*h
= Pi(3*3)*7/3 = 4.71
Answer A

Answer 2

Hence, it will take 4.71 minutes for all the liquid in the funnel to pass through the nozzle.

Explanation:

A cone shaped funnel has a radius(r) of 3 inches and a height(h) of 7 inches.

Now, the volume(V) of the cone is given as:

`V=(1)/(3)* (\pi r^2h)`

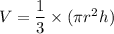
Hence, on putting the value of r and h in the formula of volume we obtain the volume of cone funnel as:

`V=(1)/(3)* (3.14* (3)^2* 7)\\\\\\V=(1)/(3)* (197.82)\\\\V=65.94 \ in^3`

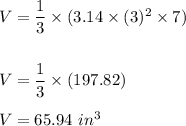
If the liquid drips at the rate of 14 cubic inches per minute.

i.e. for 14 cubic inches it takes 1 minutes.

Now for 1 cubic inches it will take:

`(1)/(14) \ min.`

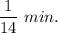
Hence, for all the liquid ( i.e. 65.94 cubic inches) to pass the nozzle is the time taken is:

`(65.94)/(14)\ min.\\\\=4.71\ min.`

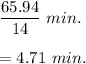
Hence, it will take 4.71 minutes for all the liquid in the funnel to pass through the nozzle.