Question

Scientists studied two animal populations. Function f(x) = 830(0.8)^x models a bear population in a given region x years after the study began. The table models the cougar population in the same region.

Year after study began: 0, 1, 2, 6, 15
Cougar population: 790, 735, 683, 511, 266
In the year the study began, how many more bears than cougars were in the given region.

Answer 1

Cougar population was 790 at the beginning
830-790=40

Answer 2

There were 40 more bears than cougars when the study started.

Explanation:

Givens:

• 
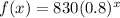  `f(x)=830(0.8)^(x)`; where
  `x` refers to years after the study began, about bear population.
• Table given is for cougar population.

So, the problem is asking how many more bears than cougars were in the given region. From the table, we know that there where 790 cougar when the study started.

Now, we have to calculate the initial condition of the function, because it's modelling bear population. Initial condition means when the study started, which is when
`x=0`.

So, we have:

`f(0)=830(0.8)^(0)=830(1)=830`

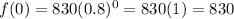
So, there were 830 bears when the study started.

If we compare, we find that there were 40 more bears than cougars when the study started, because 830-790 = 40.