Question

How do I solve this

Answer 1

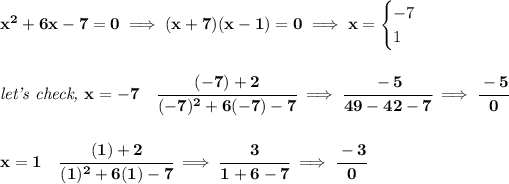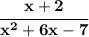
`\bf \cfrac{x+2}{x^2+6x-7}` so, that function is "defined", ok, what values of "x" are not in the domain, namely, what values can "x" take on and not make the function "undefined", well, you know, if we end up with a 0 at the denominator, like
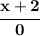
`\bf \cfrac{x+2}{0}` then, we'd have an "undefined" expression...so... any values of "x" that make the denominator 0, are not really the ones we want, and thus they'd be excluded from the domain.


so, hmm which are those? let's check, let's set the denominator to 0, and solve for "x".


`\bf x^2+6x-7=0\implies (x+7)(x-1)=0\implies x= \begin{cases} -7\\ 1 \end{cases} \\\\\\ \textit{let's check, } x=-7\quad \cfrac{(-7)+2}{(-7)^2+6(-7)-7}\implies \cfrac{-5}{49-42-7}\implies \cfrac{-5}{0} \\\\\\ x=1\quad \cfrac{(1)+2}{(1)^2+6(1)-7}\implies \cfrac{3}{1+6-7}\implies \cfrac{-3}{0}`