
notice, the tangent has a negative sign, for that to happen, either the numerator or denominator must be negative, who may that be? well, we know the angle is in the II quadrant, on the II quadrant, the cosine or x-coordinate (adjacent side) is negative, so, is the adjacent.
that means, the opposite side is 4 and the adjacent one is -3
well, let's find the hypotenuse
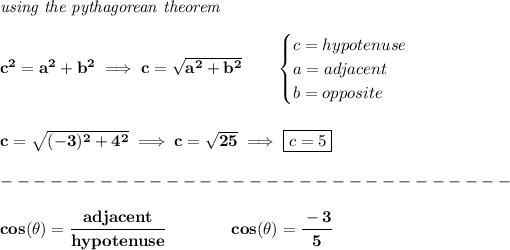
bear in mind that, the square root will give use +/- roots, however, in the case of the hypotenuse, is just the radius unit, thus is never negative.