Question

Hiroto’s texting plan costs $20 per month, plus $0.05 per text message that is sent or received. Emilia’s plan costs $10 per month and $0.25 per text. Using the graph below, which statement is true? Hiroto’s plan costs more than Emilia’s plan when more than 50 texts are sent. Both plans cost the same when 22 texts are sent. Emilia’s plan costs more than Hiroto’s plan when more than 22 texts are sent. Both plans cost the same when 50 texts are sent

Answer 1

d

Explanation:

took the test yahoot

Answer 2

Let's turn that into a linear system:

`\left \{ {{y=0.05x+20} \atop {y=0.25x+10}} \right.`
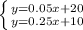
Set the equations equal to each other and solve:

`$0.05x+20=0.25x+10$`

`$0.2x=10$`

`$x=50$`
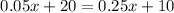
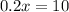
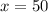
We then plug in to get
`$y$`:

`$0.25(50)+10=22.5$`
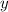
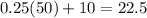
The solution to the system is
`\left \{ {{x=50} \atop {y=22.5}} \right.`.
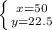
Now, let's turn our attention to the statements.
The first one is false: Emilia's rate is higher, and the two plans cost the same at 50 texts, after which point Hiroto's plan becomes cheaper!
The second one is also false: we already figured out that the lines intersect at
`$x=50$`.
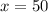
The third statement is also false: as above, the lines intersect at
`$x=50$`.
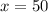
The fourth statement is true: the lines intersect at
`$x=50$`.

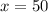
In conclusion, the fourth statement - "Both plans cost the same when 50 texts are sent" - is true.