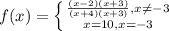Question

Give an example of a function with both a removable and a non-removable discontinuity.

Answer 1

An example of this is

F(x) = (x-2)/((x-2)(x-3))

2 is removable discontinuity

3 is non-removable discontinuity

Explanation:

Answer 2

removable discontinuity would be like imagine the graph y=3x+2, but at x=1, at the point (1,5), there is a hole, instead, there is a point at (1,10)
you can see the point there and you can remove it and put it up there

non removable is like when you have an assemtote

ok, I'll make an example using my knowlege
we wil make a term that will cancel out from top and bottom of the fraction so we get a hole
also, we need the same degree
so our function will be
`f(x)=((x-2)(x+3))/((x+4)(x+3))`
as you can see, the x+3 will cancel out leaving a hole at x=-3 (the hole is at (-3,-5) )
and the assemtote is at y=1
to make a removable discontiniuty, make a piecewise function that defines x=-3 as any number other than -5 (let's say 10

like so

`f(x)=\left \{ {{((x-2)(x+3))/((x+4)(x+3)),x \\eq -3} \atop {x=10,x=-3}} \right.`