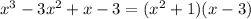Answer:
The complete factorization of the given polynomial is:
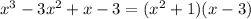
Step-by-step explanation:
Factorization of a polynomial--
It means that the polynomial could be expressed as the product of distinct factors containing the rational roots of the polynomial.
We are given a polynomial expression as:
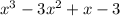
Now, it could be factorized as follows:

Now, we know that the expression:
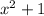 do not have a rational root.
do not have a rational root.
Hence, the complete factorization is: