Question

A sound wave is modeled with the equation y = 1/4 cos 2pi/3 theta .

A. Find the period. Explain your method.
B. Find the amplitude. Explain your method.
C. What is the equation of the midline? What does it represent?

Answer 1

`\bf \qquad \qquad \qquad \qquad \textit{function transformations} \\ \quad \\ % function transformations for trigonometric functions \begin{array}{rllll} % left side templates f(x)=&{{ A}}sin({{ B}}x+{{ C}})+{{ D}} \\\\ f(x)=&{{ A}}cos({{ B}}x+{{ C}})+{{ D}}\\\\ f(x)=&{{ A}}tan({{ B}}x+{{ C}})+{{ D}} \end{array} \\\\ -------------------\\\\`


`\bf \bullet \textit{ stretches or shrinks}\\ \left. \qquad \right. \textit{horizontally by amplitude } |{{ A}}|\\\\ \bullet \textit{ flips it upside-down if }{{ A}}\textit{ is negative}\\ \left. \qquad \right. \textit{reflection over the x-axis} \\\\ \bullet \textit{ flips it sideways if }{{ B}}\textit{ is negative}\\ \left. \qquad \right. \textit{reflection over the y-axis}`


`\bf \bullet \textit{ horizontal shift by }\frac{{{ C}}}{{{ B}}}\\ \left. \qquad \right. if\ \frac{{{ C}}}{{{ B}}}\textit{ is negative, to the right}\\\\ \left. \qquad \right. if\ \frac{{{ C}}}{{{ B}}}\textit{ is positive, to the left}\\\\ \bullet \textit{vertical shift by }{{ D}}\\ \left. \qquad \right. if\ {{ D}}\textit{ is negative, downwards}\\\\ \left. \qquad \right. if\ {{ D}}\textit{ is positive, upwards}\\\\ \bullet \textit{function period or frequency}\\`


`\bf \left. \qquad \right. \frac{2\pi }{{{ B}}}\ for\ cos(\theta),\ sin(\theta),\ sec(\theta),\ csc(\theta)\\\\ \left. \qquad \right. \frac{\pi }{{{ B}}}\ for\ tan(\theta),\ cot(\theta)`

now, with that template in mind, let's see


`\bf \begin{array}{llll} y=&(1)/(4)cos&\left( (2\pi )/(3)\theta \right)\\ &\uparrow &\quad \uparrow\\ &A&\quad B \end{array} \\\\ -------------------------------\\\\ A)\qquad period=\cfrac{2\pi }{B}\implies \cfrac{2\pi }{(2\pi )/(3)}\implies \cfrac{(2\pi)/(1) }{(2\pi )/(3)}\implies \cfrac{2\pi }{1}\cdot \cfrac{3}{2\pi }`

and surely you know how much that is

for part B)... well, is right there, from the template what A is

for part C)

well, the equation has no vertical shifting, so the midline is the same as for the parent function cos(θ).

Answer 2

A) Period = 3

B) Amplitude =
`(1)/(4)`

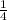
C) The equation of midline y=0

Explanation:

Given : A sound wave is modeled with the equation
`y =(1)/(4)cos ((2\pi)/(3)) \theta`

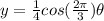
To find :

A) Period

B)Amplitude

C) The equation of Midline

Solution :

The general formula for cosine is:

`y=Acos(Bx)+C`

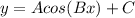
Where A is Amplitude

`B=\frac{2\pi}{\text{Period}}`

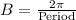
C is Mid line

Comparing the given function with general form of cosine we get,

`y =(1)/(4)cos ((2\pi)/(3)) \theta`

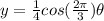
A) Period -
`B=(2\pi)/(3)`

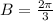
and we know,
`B=\frac{2\pi}{\text{Period}}`

`(2\pi)/(3)=\frac{2\pi}{\text{Period}}`

`\text{Period}=(2\pi* 3)/(2\pi)`

`\text{Period}=3`

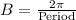
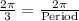
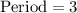
B) Amplitude-
`A=(1)/(4)`

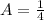
C) The equation of midline

Midline is C=0

The equation of midline is y=0.