Question

Raj fully simplified the polynomial and then put it in standard form with the last term being 6y3. 2x2y + 8x3 – xy2 – 2x3 + 3xy2 + 6y3 What is the first term of the polynomial Raj ended up with?

a 6x3
b 8x3
c 2xy2
d 3xy2

Answer 1

The first term of the polynomial Raj ended up with is A)6x3

Explanation:

Raj wants to simplify the polynomial and then put it in the standard form with last term 6y3. The first step is to order the polynomial in ascending order of y because the last term must be 6y3. Then, we can sum similar terms, which share the same letters and the same exponents.

Original polynomial:

2x^2 y + 8x^3 - xy^2 - 2x^3 + 3xy^2 + 6y^3

Order the polynomial in ascending order of y

8x^3 - 2x^3 + 2x^2y + 3xy^2 - xy^2 + 6y^3

Simplify similar terms:

6x^3 + 2x^2y + 2xy^2 + 6y^3 --> Polynomial Raj ended up with.

Finally, we can conclude that the first term of the polynomial Raj ended up with is A)6x3

Answer 2

Answer: The correct option is (a).
`6x^3.`

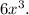
Explanation: Given that Raj fully simplifies the following polynomial and put it in standard form.

`P=2x^2y+8x^3-xy^2-2x^3+3xy^2+6y^3.`

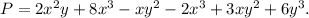
We are to find the first term of his polynomial Raj ended up with if the last term he wrote was
`6y^3.`

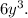
We know that

if all the terms of a POLYNOMIAL in two variables x and y has same degree, then in the standard form, it can be written in the descending power of x and ascending power of y,

or, ascending powers of x and descending powers of y.

Since all the terms in Raj's polynomial is of degree 3, and the last term is [/tex]6y^3,[/tex] which contains the highest power of y.

So, the polynomial has ascending powers of y, and consequently, it will have descending powers of x.

So, the polynomial in standard form will be

`P=2x^2y+8x^3-xy^2-2x^3+3xy^2+6y^3\\\\\Rightarrow P=6x^3+2x^2y+2xy^2+6y^3.`

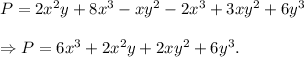
Therefore, the first term in Raj's polynomial is

`6x^3.`

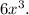
Option (a) is correct.