Question

The graph of the function f(x) = (x +2)(x + 6) is shown below. What is true about the domain and range of the function? The domain is all real numbers, and the range is all real numbers greater than or equal to –4. The domain is all real numbers greater than or equal to –4, and the range is all real numbers. The domain is all real numbers such that –6 ≤ x ≤ –2, and the range is all real numbers greater than or equal to –4. The domain is all real numbers greater than or equal to –4, and the range is all real numbers such that –6 ≤ x ≤ –2.

Answer 1

the answer is The domain is all real numbers, and the range is all real numbers greater than or equal to –4.

Answer 2

Answer: The domain is all real numbers, and the range is all real numbers greater than or equal to –4.

Explanation:

Since, the given function is,

f(x) = (x+2)(x+6)

⇒
`f(x) = x^2 + 8x + 12`

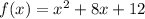
Which is the equation of parabola, ( that opened up)

Since, the vertex of the parabola is (-4,-4)

Therefore, the value of y will be not less than -4 ( because it is an upward parabola)

Thus, the range of the given function is all real number greater than or equal to –4.

Also, we know that the domain of all parabola is always the set of real numbers.

Thus, the domain of the given function is the set of all real numbers.

Therefore, first option is correct.